Deep Learning with Python
By Vihar Kurama
The human brain imitation.

The main reason behind deep learning is the idea that, artificial intelligence should draw inspiration from the brain. This perspective gave rise to the “Neural Network” terminology. The brain contains billions of neurons with tens of thousands of connections between them. Deep learning algorithms resemble the brain in many conditions, as both the brain and deep learning models involve a vast number of computation units (Neurons) that are not extraordinarily intelligent in isolation but become intelligent when they interact with each other.
I think people need to understand that deep learning is making a lot of things, behind-the-scenes, much better. Deep learning is already working in Google search, and in image search; it allows you to image search a term like “hug.”— Geoffrey Hinton
Neurons
The basic building block for neural networks are artificial neurons, which imitate human brain neurons. These are simple, powerful computational units that have weighted input signals and produce an output signal using an activation function. These neurons are spread across the several layers in the neural network.
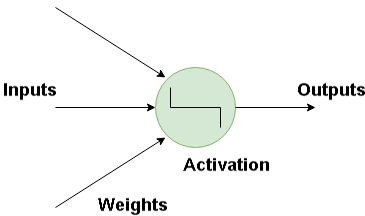
How Does Artificial Neural Network Works?
Deep learning consists of artificial neural networks that are modelled on similar networks present in the human brain. As data travels through this artificial mesh, each layer processes an aspect of the data, filters outliers, spots familiar entities, and produces the final output.
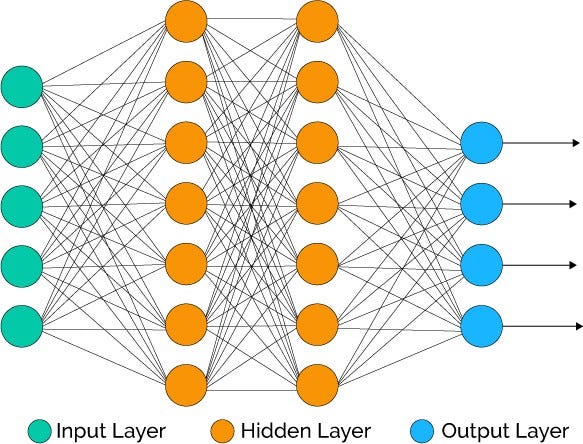
Input layer : This layer consists of the neurons that do nothing than receiving the inputs and pass it on to the other layers. The number of layers in the input layer should be equal to the attributes or features in the dataset.
Output Layer:The output layer is the predicted feature, it basically depends in the type of model you’re building.
Hidden Layer: In between input and output layer there will be hidden layers based on the type of model. Hidden layers contain vast number of neurons. The neurons in the hidden layer apply transformations to the inputs and before passing them. As the network is trained the weights get updated, to be more predictive.
Neuron Weights
Weights refer to the strength or amplitude of a connection between two neurons, if you are familiar with linear regression you can compare weights on inputs like coefficients we use in a regression equation.Weights are often initialized to small random values, such as values in the range 0 to 1.
Feedforward Deep Networks
Feedforward supervised neural networks were among the first and most successful learning algorithms. They are also called deep networks, multi-layer Perceptron (MLP), or simply neural networks and the vanilla architecture with a single hidden layer is illustrated. Each Neuron is associated with other neuron with some weight,
The network processes the input upward activating neurons as it goes to finally produce an output value.This is called a forward pass on the network.
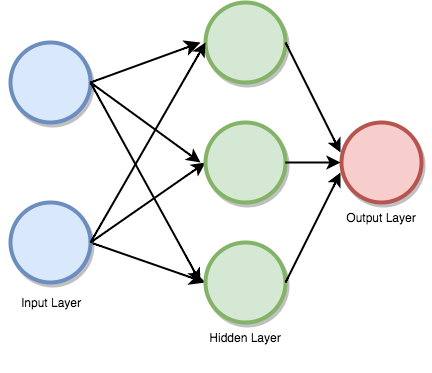
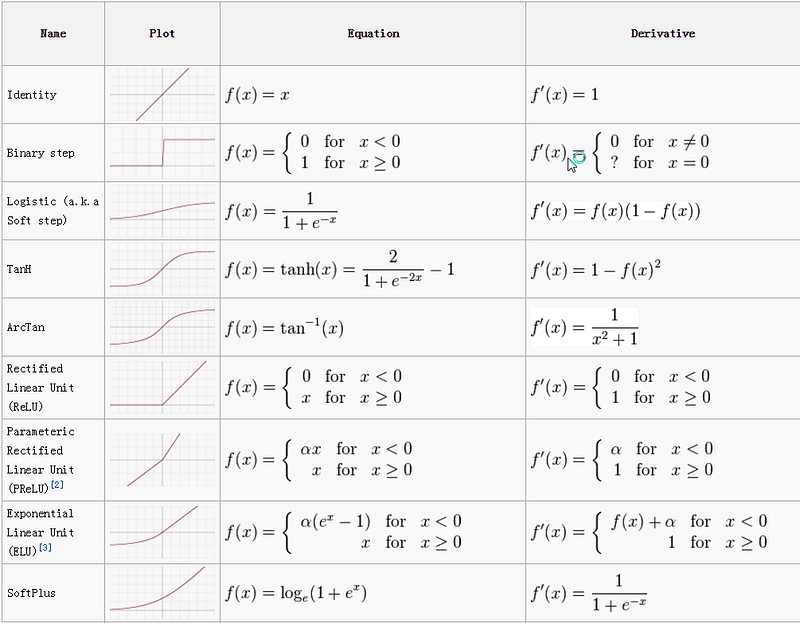
Activation Function
An activation function is a mapping of summed weighted input to the output of the neuron. It is called an activation/ transfer function because it governs the inception at which the neuron is activated and the strength of the output signal.
Mathematically,
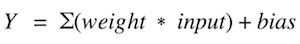
We have many activation functions, out of which most used are relu, tanh, solfPlus.
The cheat sheet for activation functions in given below.
Back Propagation
The predicted value of the network is compared to the expected output, and an error is calculated using a function. This error is then propagated back within the whole network, one layer at a time, and the weights are updated according to the value that they contributed to the error. This clever bit of math is called the Back-Propagation algorithm. The process is repeated for all of the examples in your training data. One round of updating the network for the entire training dataset is called an epoch. A network may be trained for tens, hundreds or many thousands of epochs.
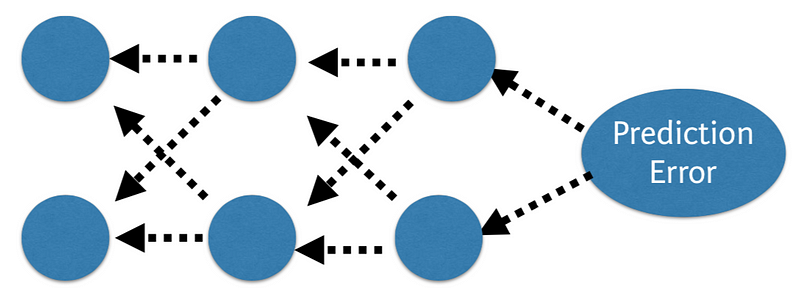
Cost Function and Gradient Descent
The cost function is the measure of “how good” a neural network did for it’s given training input and the expected output. It also may depend on attributes such as weights and biases.
A cost function is single-valued, not a vector because it rates how well the neural network performed as a whole. Using the Gradient Descent optimization algorithm, the weights are updated incrementally after each epoch.
Compatible Cost Function:
Mathematically,
Sum of squared errors (SSE)
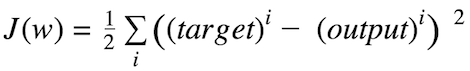
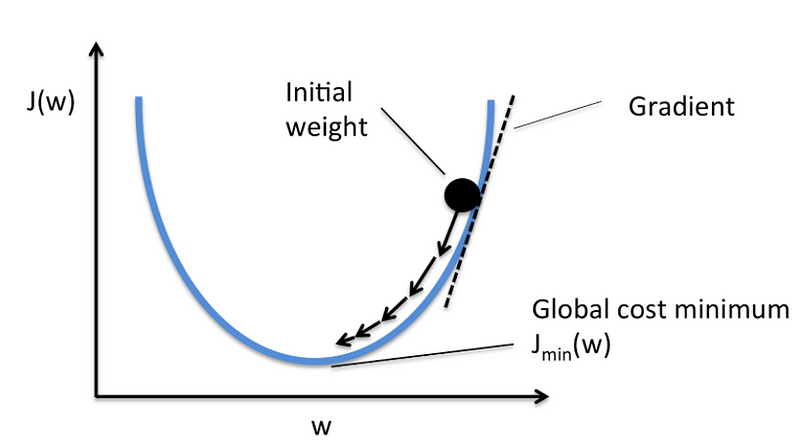
The magnitude and direction of the weight update is computed by taking a step in the opposite direction of the cost gradient.
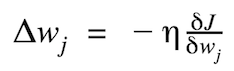
where Δw is a vector that contains the weight updates of each weight coefficient w, which are computed as follows:
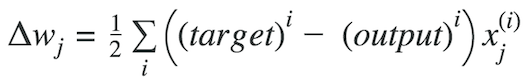
Graphically, considering cost function with single coefficient
We calculate the gradient descent until the derivative reaches the minimum error, and each step is determined by the steepness of the slope (gradient).
Multi Layer Perceptrons (Forward Propagation)
This class of networks consists of multiple layers of neurons, usually interconnected in a feed-forward way (moving in a forward direction). Each neuron in one layer has direct connections to the neurons of the subsequent layer. In many applications, the units of these networks apply a sigmoid or relu (Rectified Linear Activation) function as an activation function.
Now consider a problem to find the number of transactions, given accounts and family members as input.
To solve this first, we need to start with creating a forward propagation neural network. Our Input layer will be the number of family members and accounts, the number hidden layers are one, and the output layer will be the number of transactions.
Given weights as shown in the figure from the input layer to hidden layer with the number of family members 2 and number of accounts 3 as inputs.
Now the values of hidden layer (i, j) and output layer (k) will be calculated using using forward propagation by the following steps.
Process
- Multiply — add process.
- Dot product (Inputs * Weights).
- Forward propagation for one data point at a time.
- Output is the prediction for that data point.
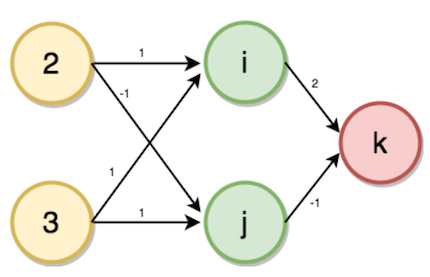
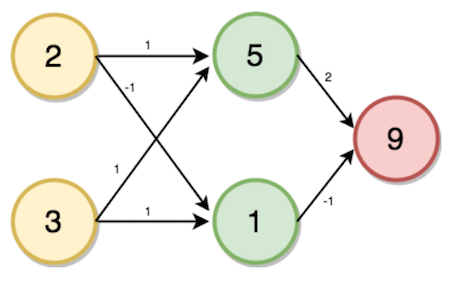
Value of i will be calculated from input value and the weights corresponding to the neuron connected.
i = (2 * 1) + (3 * 1)
→ i = 5
Similarly,
j = (2 * -1) + (3 * 1)
→ j = 1
K = (5 * 2) + (1 * -1)
→ k = 9
Solving the Multi Layer Perceptron problem in Python
import numpy as np
print("Enter the two values for input layers")
print('a = ')
a = int(input())
# 2
print('b = ')
b = int(input())
# 3
input_data = np.array([a, b])
weights = {
'node_0': np.array([1, 1]),
'node_1': np.array([-1, 1]),
'output_node': np.array([2, -1])
}
node_0_value = (input_data * weights['node_0']).sum()
# 2 * 1 +3 * 1 = 5
print('node 0_hidden: {}'.format(node_0_value))
node_1_value = (input_data * weights['node_1']).sum()
# 2 * -1 + 3 * 1 = 1
print('node_1_hidden: {}'.format(node_1_value))
hidden_layer_values = np.array([node_0_value, node_1_value])
output_layer = (hidden_layer_values * weights['output_node']).sum()
print("output layer : {}".format(output_layer))
dl_multilayer_perceptron.py hosted with ❤ by GitHub
$python dl_multilayer_perceptron.py
Enter the two values for input layers
a =
3
b =
4
node 0_hidden: 7
node_1_hidden: 1
output layer : 13
Using Activation Function
For neural Network to achieve their maximum predictive power we need to apply an activation function for the hidden layers.It is used to capture the non-linearities. We apply them to the input layers, hidden layers with some equation on the values.
Here we use Rectified Linear Activation (ReLU)
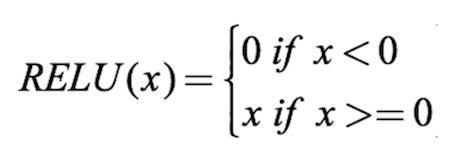
import numpy as np
print("Enter the two values for input layers")
print('a = ')
a = int(input())
# 2
print('b = ')
b = int(input())
weights = {
'node_0': np.array([2, 4]),
'node_1': np.array([[4, -5]]),
'output_node': np.array([2, 7])
}
input_data = np.array([a, b])
def relu(input):
# Rectified Linear Activation
output = max(input, 0)
return(output)
node_0_input = (input_data * weights['node_0']).sum()
node_0_output = relu(node_0_input)
node_1_input = (input_data * weights['node_1']).sum()
node_1_output = relu(node_1_input)
hidden_layer_outputs = np.array([node_0_output, node_1_output])
model_output = (hidden_layer_outputs * weights['output_node']).sum()
print(model_output)
dl_fp_activation.py hosted with ❤ by GitHub
$python dl_fp_activation.py
Enter the two values for input layers
a =
3
b =
4
44
Developing First Neural Network with Keras
About Keras:
Keras is a high-level neural networks API, written in Python and capable of running on top of TensorFlow, CNTK, or Theano.
To install keras on your machine using PIP, run the following command.
sudo pip install keras
Steps to implement your deep learning program in Keras
- Load Data.
- Define Model.
- Compile Model.
- Fit Model.
- Evaluate Model.
- Tie It All Together.
Developing your Keras Model
Fully connected layers are described using the Dense class. We can specify the number of neurons in the layer as the first argument, the initialisation method as the second argument as init and determine the activation function using the activation argument. Now that the model is defined, we can compile it. Compiling the model uses the efficient numerical libraries under the covers (the so-called backend) such as Theano or TensorFlow. So far we have defined our model and compiled it set for efficient computation. Now it is time to run the model on the PIMA data. We can train or fit our model on our data by calling the fit() function on the model.
Let’s get started with our program in KERAS,
# Importing Keras Sequential Model
from keras.models import Sequential
from keras.layers import Dense
import numpy
# Initializing the seed value to a integer.
seed = 7
numpy.random.seed(seed)
# Loading the data set (PIMA Diabetes Dataset)
dataset = numpy.loadtxt('datasets/pima-indians-diabetes.csv', delimiter=",")
# Loading the input values to X and Label values Y using slicing.
X = dataset[:, 0:8]
Y = dataset[:, 8]
# Initializing the Sequential model from KERAS.
model = Sequential()
# Creating a 16 neuron hidden layer with Linear Rectified activation function.
model.add(Dense(16, input_dim=8, init='uniform', activation='relu'))
# Creating a 8 neuron hidden layer.
model.add(Dense(8, init='uniform', activation='relu'))
# Adding a output layer.
model.add(Dense(1, init='uniform', activation='sigmoid'))
# Compiling the model
model.compile(loss='binary_crossentropy',
optimizer='adam', metrics=['accuracy'])
# Fitting the model
model.fit(X, Y, nb_epoch=150, batch_size=10)
scores = model.evaluate(X, Y)
print("%s: %.2f%%" % (model.metrics_names[1], scores[1] * 100))
keras_pima.py hosted with ❤ by GitHub
$python keras_pima.py
768/768 [==============================] - 0s - loss: 0.6776 - acc: 0.6510
Epoch 2/150
768/768 [==============================] - 0s - loss: 0.6535 - acc: 0.6510
Epoch 3/150
768/768 [==============================] - 0s - loss: 0.6378 - acc: 0.6510
.
.
.
.
.
Epoch 149/150
768/768 [==============================] - 0s - loss: 0.4666 - acc: 0.7786
Epoch 150/150
768/768 [==============================] - 0s - loss: 0.4634 - acc: 0.773432/768
[>.............................] - ETA: 0sacc: 77.73%
The neural network trains until 150 epochs and returns the accuracy value.

My husband and i have been very contented Emmanuel could complete his research through the entire ideas he discovered out of your blog. It’s not at all simplistic to simply continually be releasing strategies that many some other people might have been selling. And now we take into account we’ve got you to be grateful to for that. Those illustrations you have made, the easy website menu, the friendships your site make it easier to engender – it’s got mostly remarkable, and it’s leading our son in addition to our family understand this subject matter is amusing, and that’s extremely… Read more »
I together with my guys came checking out the best guides located on your web site and then all of a sudden I had a terrible feeling I never thanked the site owner for those tips. Most of the people are actually as a consequence happy to learn them and have in effect absolutely been loving them. Thank you for being very helpful as well as for deciding on this form of important resources most people are really eager to discover. My very own honest apologies for not expressing gratitude to earlier.
My spouse and i ended up being so joyous when Edward managed to complete his inquiry from your precious recommendations he acquired from your web page. It is now and again perplexing just to find yourself handing out solutions which often others may have been trying to sell. Therefore we do understand we’ve got you to appreciate for that. The most important illustrations you have made, the straightforward web site navigation, the friendships you will help to instill – it’s many awesome, and it’s aiding our son and our family reason why that idea is awesome, which is certainly especially… Read more »
A lot of thanks for all of the hard work on this blog. Ellie really likes doing internet research and it is obvious why. All of us learn all relating to the powerful mode you deliver both interesting and useful suggestions on your web site and as well invigorate contribution from other people on the topic while my princess is without question becoming educated a lot of things. Have fun with the remaining portion of the new year. You’re the one doing a terrific job.
I want to get across my gratitude for your generosity in support of men and women who require help on this particular area of interest. Your real commitment to passing the message across turned out to be definitely interesting and have continuously enabled many people like me to achieve their targets. This helpful guidelines entails so much a person like me and far more to my office workers. Warm regards; from each one of us.
Thank you so much for giving everyone an extremely pleasant opportunity to discover important secrets from this website. It is usually so brilliant and also full of a good time for me and my office peers to visit the blog a minimum of 3 times in one week to find out the newest issues you will have. Of course, I am also actually fascinated for the terrific strategies served by you. Some 1 points in this posting are honestly the most impressive we’ve ever had.
My husband and i were quite excited when Peter managed to complete his inquiry from the ideas he obtained out of your web pages. It is now and again perplexing just to possibly be handing out information and facts which the rest may have been trying to sell. We do understand we’ve got the writer to appreciate for this. Most of the explanations you made, the straightforward website navigation, the relationships you make it easier to foster – it is mostly unbelievable, and it’s really leading our son in addition to our family do think that idea is fun, and… Read more »
I am only commenting to make you be aware of of the really good discovery my friend’s child developed reading through the blog. She came to find numerous details, with the inclusion of what it’s like to have an amazing coaching style to get many others without hassle know precisely several problematic subject areas. You truly exceeded readers’ desires. Thanks for offering those precious, trusted, educational and unique guidance on this topic to Ethel.